Chang Luo
Author Image

© 2024 Chang Luo

像搭积木一样搭神经网络

Jul 7, 2024 in DEEPLEARNING
dropout decay
3 min read

搭积木的时候，需要将不同类型的积木搭在一起：门框、窗子、走廊、屋顶。对每一种类型的积木，又有多种变体可供选择。比如，屋顶可以用文艺复兴风格，也可以用中式庭园风格。神经网络也是，学神经网络，本质上就是认识各种各样“积木”的过程。

GitHub 项目地址：dl-tricks/note.ipynb

一、必要组件

1.1 从 MLP 说起

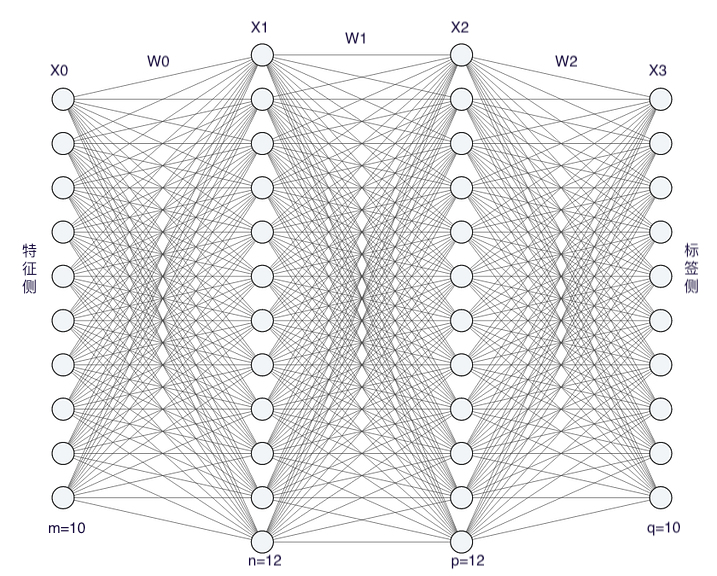
我们从最简单的深度神经网络 多层感知机 (MLP) 开始说起。麻雀虽小，五脏俱全。了解数据如何在 MLP 中流动，就能大致勾勒一个神经网络的 必要组件。

下图是一个 4 层感知机，左边是特征，右边是标签。训练开始时，样本数据先从左到右做 正向传播。待数据流到右侧，用 损失函数 计算损失。此时损失是一个标量，而最后一层的节点权重 $W$ 是一个矩阵，标量对矩阵的偏导是矩阵。优化器 会用大小合适的梯度矩阵，沿负梯度方向逐层反向更新权重 $W$。这样下一 批量 (batch) 数据进入网络时，正好能用上一轮更新后的参数做正向传播。

1.2 DataLoader

样本是有限的，为了让模型获得最强性能，必须榨干每个样本的价值。

因此在训练中，一个样本往往要复用多次。DataLoader 就在做这样一件事。它把数据编排成一个个批量，并构建一个迭代器。每次调用它，会返回一个从第一个批量开始遍历的迭代器。这个特性使得复用样本变得更加方便。

原生的 PyTorch DataLoader 很复杂，让我们来实现一个野生 DataLoader：

import math
import torch

class DataLoader:
    def __init__(self, data: list, batch_size: int):
        self.i = 0
        self.batch_size = batch_size
        self.batch_num = math.floor(len(data) / batch_size)
        self._data = self.gen_batch(data)

    def gen_batch(self, data):
        lst = []
        s = self.batch_size
        for i in range(self.batch_num):
            start, end = s * i, s * (i + 1)
            X = torch.tensor([e[0] for e in data[start:end]])
            y = torch.tensor([e[1] for e in data[start:end]])
            lst.append((X, y))

        return lst

    def __iter__(self):
        self.i = 0
        return self

    def __next__(self):
        if self.i < len(self._data):
            self.i += 1
            return self._data[self.i - 1]
        else:
            raise StopIteration

假设有 2560 个样本。计划分成 10 个批量，则每批量有 256 个样本。我们可以用上面的野生 DataLoader 加载这些样本。

# 构造符合 f(a, b) = \frac{a^2 - b^2}{a^2 + b^2} + \epsilon 函数的样本生成
sample_num, batch_size = 2560, 10
X = [(random.random(), random.random()) for e in range(sample_num)]
y = map(lambda e: ((e[0]**2 - e[1]**2) / (e[0]**2 + e[1]**2)) + (random.random() / 100), X)

raw_data = list(zip(X, y))

# 输出一个批量的数据
for X, y in DataLoader(data=raw_data, batch_size=batch_size):
    print(f'X: {X}')
    print(f'y: {y}')
    break

在实际训练过程中，如果把全部 10 个批量的数据全训了一遍，就叫完成一个轮次 (epoch) 的训练。深度神经网络通常需要多个轮次训练才会收敛。

Note: 为什么要做成批量？因为批量计算提高了反向传播的效率。你可以问 GPT：批量随机梯度下降比随机梯度下降好在哪儿？

1.3 神经元里发生了什么

为了考察神经元里发生了什么。我们假设输入样本有 10 个特征 (features). 我们构建一个四层 MLP，假定各层神经元数量如下：

[Layer 0] 第一层维数为 10
[Layer 1] 第二层维数为 12
[Layer 2] 第三层维数为 12
[Layer 3] 第四层维数为 10

在设计各层神经元数量时，需要满足一些客观条件：

  • 第一层神经元数量需与样本特征数相同
  • 最后一层神经元数量需与预测的类别数相同
  • 中间隐藏层的神经元数量比较自由，可以灵活地调整

现在，我们来考虑一个样本在 MLP 的前两层做正向传播的情况：

第一层：

把样本的 10 个特征直接填入 10 个神经元就好了。

# 原始特征
features = ["张", "女性", 143.0, "国际贸易", 97.0, \
            88.5, 95.0, 79.0, 91.0, 70.0]

# 经过 encoder 编码后
features = [33, 1, 143.0, 1002, 97.0, \
            88.5, 95.0, 79.0, 91.0, 70.0]

# 把特征注入对应神经元
x_00, x_01, x_02, x_03, x_04, x_05, x_06, x_07, x_08, x_09 = *features

第二层：

第二层第 i 个神经元的值 $x_{1i}$，可以看作是由第一层神经元的值 $x_{0i} (i \in [0, 9])$ 经过 线性变换 -> 加偏置项 -> 过激活函数 得到的。

公式表达如下：

$$ x_{1i} = ReLU (W_{0i} X_0 + b_{0i}) $$

其中：

符号 解释
$ReLU$ 是激活函数
$W_{0i}$ 第 2 层第 i 个神经元上的可学习权重，是长为 10 的一维向量
$X_0$ 第 1 层所有神经元 x 值 concat 成的向量，是长为 10 的一维向量
$b_{0i}$ 第 2 层第 i 个神经元上的可学习偏置，是标量
$x_{1i}$ 第 2 层第 i 个神经元的值，是标量（对于最后一层，它就是输出值 $\hat{y}_{i}$）

以下三个参数可以被认为是“包含”在第 i 个神经元中：

  • $W_{0i}$: 权重
  • $b_{0i}$: 偏置
  • $x_{1i}$: 神经元的值

注意到，$W_{0i}$ 和 $b_{0i}$ 下标的第一个数字虽然是 0，并不意味着它们在 Layer 0（第一层）上，它们实际“属于”第二层的第 i 个神经元。

下图解释了这种情况形成的原因：我们认为 $x_{1i}$ 的计算过程发生在第二层中，因此 $X_0$ 被看作是来自上一层的输入。因此 $W_{0i}$ 和 $b_{0i}$ 也应被视为在第二层上进行更新的参数。但是计算时，这俩参数实际与 $X_0$ 发生运算，在等式中又位于 $X_0$ 那边，因此具有 0 下标.

描述信息

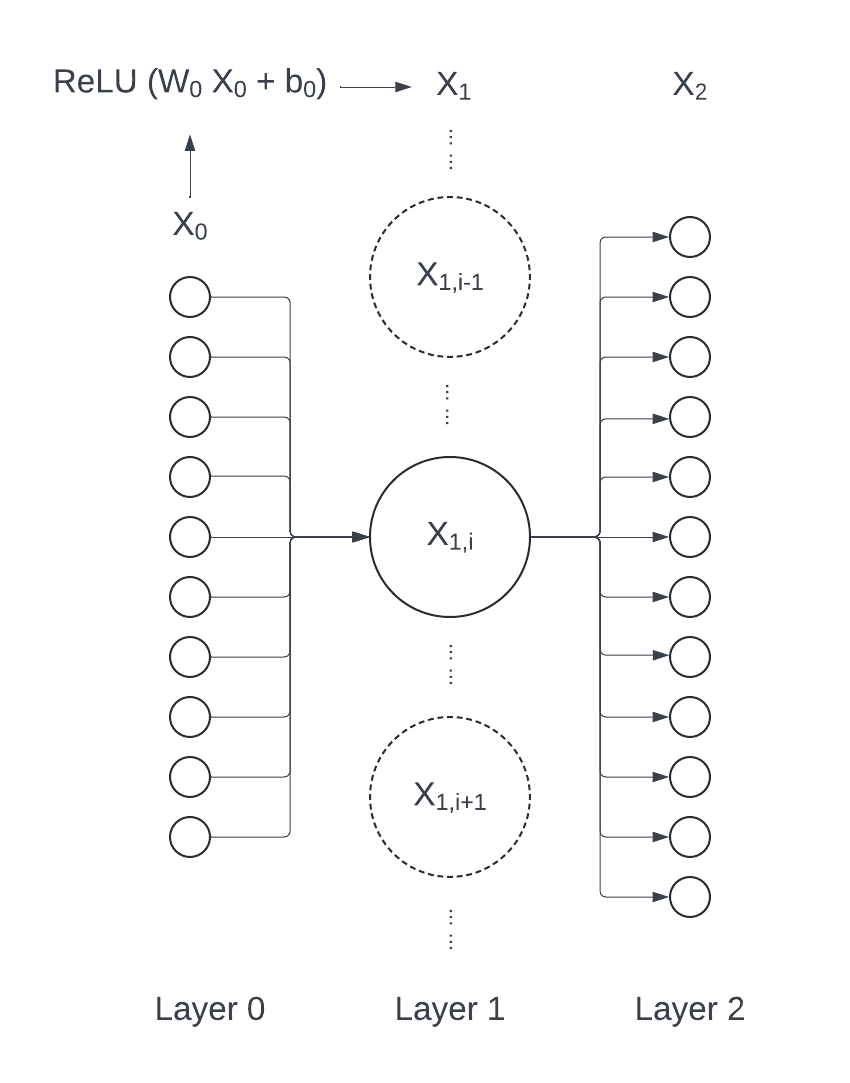
好崩溃，画个图把 Lucid 免费额度用完了 (´;ω;`)

1.4 层视角，而非神经元视角

如果从层视角，而非从神经元视角看。

我们把：

  • 第二层所有权重 $W_{00}, W_{01}, ... ... W_{09}$ concat 起来得到矩阵 $W_0$
  • 第二层所有偏置 $b_{00}, b_{10}, ... ... b_{0,11}$ concat 起来得到向量 $b_0$
  • 第一层所有神经元的值 $X_{00}, X_{01}, ... ... X_{09}$ concat 起来得到 $X_0$
  • 第二层所有神经元的值 $X_{10}, X_{11}, ... ... X_{1,11}$ concat 起来得到 $X_1$

此时，第一层到第二层的非线形变换可写作：

$$ X_1 = ReLU (W_0 X_0 + b_0) $$

二、激活函数

激活函数堪称伟大。如果说神经网络的多层架构解决了 XOR 问题，激活函数则为深度神经网络引入了非线性性，让神经网络具有拟合任意函数的能力，使其拥有了解非凸优化问题的能力。

本节介绍三种常见的激活函数：Sigmoid, Tanh, ReLU。其中 ReLU 因为计算简单，在工业界被大量使用。

2.1 Sigmoid

  • 表达式：$ sigmoid (x) = \frac{1}{1 + e^{-x}} $
  • 值域：$(0, 1)$
  • 特性：导数存在且处处可微。但在输入值很大或很小的情况下，梯度接近于零，导致梯度消失的问题。且输出不是零均值，可能会影响下一层的收敛速度。

2.2 Tanh

  • 表达式：$ \tanh(x) = \frac{1 - e^{-2x}}{1 + e^{-2x}} $
  • 值域：$(-1, 1)$
  • 特性：与 Sigmoid 函数相似，存在梯度消失问题。但相比 Sigmoid 函数，输出值更接近于零均值，有助于加快收敛速度。

2.3 ReLU

  • 表达式：$ ReLU (x) = \max(0, x) $
  • 值域：$[0, +\infty)$
  • 特性：简单高效，计算速度快。当输入为正数时，梯度为 1，可避免梯度消失问题；当输入为负数时，梯度为 0，意味着不再激活，即神经元死亡。输出不是归一化的，可能需要额外的规范化技术。

2.4 Softmax

  • 表达式：$\operatorname{softmax}(\mathbf{X})_{i j}=\frac{\exp \left(\mathbf{X}_{i j}\right)}{\sum_k \exp \left(\mathbf{X}_{i k}\right)}$
  • 值域：输出是一个概率分布，所有元素和为 1
  • 特性：可将任意实数向量转化为概率分布向量，常用于分类模型输出层的激活函数。

三、损失函数

对于不同的任务，常用损失函数也不同。分类任务常用交叉熵损失；回归任务常用均方误差损失。

3.1 交叉熵损失

交叉熵损失（Cross Entropy Loss）用于衡量两个分布的差异。差异越大，则损失函数的值越大。

下面给出交叉熵函数的计算公式：

  1. 对于 二分类任务，假设模型正样本概率为 p，真实标号正样本概率为 q，则模型给出的预测分布和真实分布之间的交叉熵可由下式计算：

    $H(p, q) = - (p \cdot \log(q) + (1 - p) \cdot \log(1 - q))$

  2. 对于 多分类任务，假设模型预测概率分布为 P，真实标号分布为 Q，则交叉熵函数为：

    $H(P, Q) = - \sum_{i=1}^{C} (P(i) * log(Q(i)))$

写个函数验证下这件事：

3.2 均方误差

均方误差（Mean Squared Error, MSE）

四、优化器

4.1 SGD

4.2 Adam

五、链式求导

六、正则化技术

6.1 权重衰减

6.2 dropout

七、优化策略（梯度更新策略）

7.1 梯度裁剪

7.2 学习率调度

7.3 量化

八、归一化技术

8.1 批量归一化

8.2 层归一化

九、推理和可视化

ONNX + Netron

文本情感分析 SynchroTrap 算法实现